
matemáticas 4.1 y 4.3 , tercer periodo
RETO UNO
SEMANA :AGOSTO 24 - AGOSTO 28
FECHA DE ENTREGA : MÁXIMO LUNES 31 DE AGOSTO.
En este reto abordaremos , situaciones de problema con mcm y McD, clases de triángulos.
Actividad para realizar en tu cuaderno
Para tener en cuenta : cuando entre 2 ó mas cantidades(números), se busca un punto o número común(igual),quiere decir que hay que recurrir al mcm o al McD , entre esas cantidades.
El mcm se utiliza cuando se busca: el menor, el mínimo, el más pequeño, el más cercano...entre otros.
El Mcd se utiliza cuando se busca : el máximo, el más grande , el más lejos , el último ...entre otros.
Resuelvo las siguientes situaciones de problema :
Todo el proceso debe aparecer: procedimiento y respuesta.
Elementos para un mejor análisis y comprensión (guía para padres)No se escribe en el cuaderno , es para leer y poner en practica.
Como padres podemos ayudarles a ganar seguridad a la hora de enfrentarse a desafíos matemáticos y estructurar la información de forma que les permita encontrar una solución:
- Ayúdale a representar el problema
Si tu hijo no entiende el problema, no podrá resolverlo. Pídele que lea el problema en voz alta y luego pregúntale si ha entendido todas las palabras y lo que se le pide que haga. Podemos ayudarnos de lápiz y papel para dibujar los objetos o cantidades mencionadas en el problema o bien coger objetos de casa para representarlo. Esto hará que vaya desarrollando su pensamiento abstracto.
- Enséñale a comprender qué se le pide
Una vez ha representado los diferentes elementos, pídele que lea el problema de nuevo y que identifique qué tiene que resolver y qué operaciones matemáticas podrá utilizar para encontrar la solución. Es importante que conozca las operaciones matemáticas básicas como la suma, la resta, la multiplicación y la división. Puedes subrayar en el problema los datos relevantes que nos servirán para resolverlo o apuntarlos en una hoja aparte para poder trabajarlos con las operaciones por separado.
- Revisar juntos el resultado
Pídele que resuelva el problema con las operaciones que ha seleccionado. Cuando tenga la solución, pídele que vuelva a leerlo y que decida si su solución tiene sentido. En caso de que se haya equivocado, ayúdale a revisar el proceso de razonamiento para encontrar el error y corregirlo.

Carlos dispone de dos listones de madera iguales pero de longitudes 25 y 30 centímetros. Si tiene que cortarlos en trozos iguales de forma que tenga el máximo número posible de trozos, ¿ cuánto deben medir cada trazo.?

¿Cuál es el mínimo número de cajas de cada color que debe comprar Marta para tener el mismo número de lápices de ambos colores?

Antonio tiene 10 kg de cemento y 15 kg de arena , quiere preparar sacos iguales con la misma proporción de cemento y arena para guardarlos en el trastero, pero desea comprar el mínimo número posible de sacos. ¿Cuántos sacos debe comprar?

Pablo tarda minutos en dar una vuelta completa al circuito con su moto y Alberto tarda minutos. Si los dos motoristas salen de la misma línea y al mismo tiempo, ¿ En cuántos minutos se encontrarán de nuevo en la línea de salida por primera vez?
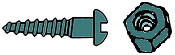
Si los tornillos se venden en cajas de unidades y las tuercas en cajas de , ¿cuántas cajas de cada uno tenemos que comprar para tener una rosca por cada tornillo?
Para escribir en tu cuaderno
CLASES DE TRIÁNGULOS


Según lados: Según lados: Según lados:
Según ángulos: Según ángulos: Según ángulos:
¡ lo has logrado!👏👏👏👏
RETO DOS
DURACIÓN:AGOSTO 7 - AGOSTO 11
FECHA MÁXIMA DE ENTREGA: LUNES 14 DE AGOSTO
| FRACCIONES |
En este reto abordaremos las fracciones y el plano cartesiano.
Para familiarizarnos con las fracciones disfrutemos los siguientes vídeos👇
¿ qué es una fracción?
Una fracción representa una parte de la unidad , dividida en partes iguales.
¿Cuáles son las partes de una fracción?
Una fracción se compone de numerador , denominador y vínculo.
Numerador: cantidad de partes que tomamos o coloreamos.
Denominador : total de partes en las que se divide la unidad.
Vinculo: linea horizontal o diagonal que separa el numerador del denominador.

Las fracciones se pueden utilizar para indicar una región y /o para representar la parte de un conjunto,
ejemplo:
la región que se indica corresponde a 2 / 5 (dos quintos) del total de partes.
la flor roja , representa 1 / 3 ( un tercio) del total de las flores.
¿Cómo leer fracciones?
Primero se lee el numerador como cardinal(normal) y luego el denominador como ordinal(medios , tercios cuartos , quintos , sextos , séptimos, octavos , novenos , décimos y a partir de 11 , se agrega la partícula avos ) , ejemplo:
¡ vamos a poner en práctica lo aprendido!
1 - escribe la fracción que representa cada imagen , señala sus términos y escribe como de lee.
2- Representa gráficamente (dibujo) las siguientes fracciones:
- 3 /9 = -8 /20=
- 5 / 12= - 2 / 3 =
-6 /10 = - 4 / 7=
3 - Escribe como fracción, según la imagen:
-
-fracción de casas con techo rojo=
- fracción de casas con techo café =
- fracción de casas con techo negro =
-fracción de casas con ventanas azules=
-fracción de casas con 2 ventanas=
4 - Escribe como fracción:
- cantidad de hombres que viven en tu casa =
- Cantidad de mujeres que viven en tu casa =
- cantidad de niños que viven en tu casa =
- cantidad de personas mayores que viven en tu casa =
¿Qué es el plano cartesiano?
El plano cartesiano está formado por 2 rectas numéricas , una horizontal , llamada eje X y una vertical llamada eje Y. En el plano cartesiano se ubican coordenadas o pares ordenados , siempre ubicando primero el del eje X y luego el del eje Y , así . (X , Y ), cada coordenada es un único punto en el plano, ejemplo:
La mosca está ubicada en el punto 6 de X y el punto 5 de Y , por lo tanto la coordenada correspondiente
(6 , 5)
↓ ↓
( x , y)
¡ vamos a practicar !
1 -De acuerdo con el plano , escribe la coordenada donde está ubicada cada imagen.
- Banco ( , )
- Depósito de basura ( , )
- Sillón ( , )
- Pintura ( , )
-Libro ( , )
- Chinche ( , )
- Bombas ( , )
2 - completo cada coordenada
¡ felicitaciones , has terminado!
RETO TRES
DURACIÓN: SEPTIEMBRE 21 –
SEPTIEMBRE 25
FECHA MÁXIMA DE ENTREGA: LUNES 28 DE SEPTIEMBRE
En este reto trabajaremos: clases de fracciones,
números mixtos, gráficas y refuerzo de operaciones básicas.
Clases de fracciones
-Fracciones
propias: Son aquellas
en las que se utiliza menos de una
unidad (el numerador es menor que
el denominador), ejemplo
se utiliza menos de una unidad
-
Fracciones impropias: son aquellas en las que se utiliza más de una unidad (numerador es mayor que el denominador), ejemplo
Se utiliza más de una unidad
Toda
fracción impropia, se puede expresar como número mixto.
El
número mixto: resulta
de dividir el numerador, entre el denominador (gráficamente, se cuentan las
unidades completas y la fracción que se tomó de la última unidad), ejemplo
Fracción impropia ⇒
6/2 = 2 1/2 ⇒ número mixto
También podemos encontrar el numero mixto por medio de la división, así:
-
fracciones iguales a la unidad o enteras : son aquellas en las que se utiliza una unidad completa
(numerador igual a denominador),
ejemplo
se utiliza la unidad entera
¡vamos
a aplicar lo aprendido!
1- completa
cada fracción y escribe si es propia, impropia o igual a la unidad.
2
-Representa gráficamente(dibujo) cada fracción, escribe como se leen y
clasifica en propias, impropias e iguales a la unidad:
- 6/7 =
- 15/20 =
- 8/8 =
- 9/6=
- 3/8 =
- 12/8 =
4 - Complete
la siguiente tabla:
|
Fracción impropia |
Gráfica |
División |
Número mixto |
|
16/9 |
|
|
|
|
8/5 |
|
|
|
|
12/7 |
|
|
|
|
7/2 |
|
|
|
|
|
|
|
|
TABLAS
DE FRECUENCIA Y GRÁFICOS
Es una ordenación de datos en forma de tabla, de unos datos estadísticos
asignándole a cada dato una frecuencia.
FRECUENCIA: cantidad de veces que se repite un dato.
MODA: corresponde al dato que más se repite
o que tiene mayor frecuencia.
Ejemplo:
|
Deporte preferido |
Personas encuestadas |
frecuencia |
|
ciclismo |
x x x x x x
xx x x x xx |
13 moda |
|
fútbol |
x x x x x x x
x x x |
10 |
|
baloncesto |
x x x x x |
5 |
|
natación |
x x |
2 |
|
total |
|
30 |
El deporte preferido, entre los encuestados es el ciclismo, porque tiene la mayor frecuencia (13), por tanto corresponde a la moda.
CLASES
DE GRÁFICAS
Los datos recopilados en la tabla de frecuencia, se pueden representar en diferentes gráficas:
ACTIVIDAD
DE APLICACIÓN
1- - Con base en el siguiente pictograma,
responde cada una de las preguntas.
2- -Con base en el siguiente pictograma,
responde:
¿Cuántos árboles corresponden a la frecuencia de cada día?
¿Cuál día corresponde a la moda (doto con mayor frecuencia)?
¿En qué día se sembraron 12 árboles?
¿Cuál fue el día menos productivo y por qué?
3-con base en la gráfica de barras
identifica:
-cantidad de
personas encuestadas --------------
-Dato que
corresponde a la moda -------------
-Mascota(s)
menos preferida -----------
4– Con base en la gráfica de líneas y puntos, coloco verdadero (v) o falso (f).
-
La moda corresponde al día Jueves( )
-
Entre el miércoles y el sábado asisten 920
trabajadores( )
-
El día martes, asisten 85 trabajadores, menos que el
miércoles ( )
- El día que más trabajadores asisten es el jueves
REFUERZO DE OPERACIONES BÁSICAS
Resuelvo las siguientes operaciones de
manera vertical, con
prueba en la resta y la división:
-
2.850 + 24.285 + 8 =
-
23.850 ÷ 9 =
-
122.280 ÷ 25 =
-
12.285 x 432 =
¡lo lograste!
RETO
CUATRO
DURACIÓN: octubre 13 – octubre 16
FECHA
LIMITE DE ENTREGA: lunes 19 de octubre
En este reto abordaremos: fracción de un número,
situaciones de problema y elaboración de gráficas (población, muestra y
varíale).
DBA –Identifica la fracción de un número.
DBA – Interpreta y representa datos descritos como puntos
en el primer cuadrante del plano cartesiano.
FRACCIÓN
DEN UN NÚMERO
Favor ver con atención el video
Para escribir en el cuaderno
Para encontrar la fracción de una cantidad, se divide la cantidad por el denominador de la fracción y el resultado, se multiplica
por el numerador, ejemplo:
3/6 de 30 = 30 ÷ 6 = 5 y 5 x 3 = 15
denominador
numerador
Entonces 3/6 de 25 = 15
ACTIVIDAD PARA RESOLVER
1-Encuentra el
resultado para cada uno de los siguientes ejercicios (debe
aparecer el proceso)
2-Resuelve las siguientes
situaciones (deben aparecer todos los
procedimientos y respuestas)
-
En el grado 4°, hay 90 estudiantes, de los cuales 2/9 son
mujeres. ¿Cuántas mujeres hay en 4°?, ¿Cuántos hombres hay en 4°?
-
María partió un pastel en 25 partes iguales, se gasta
10/25 de la torta. ¿Qué fracción de
torta se queda sin repartir?
-
Juana tiene $ 180.000, reparte entre sus hijos 4/9.
¿Cuánto dinero repartió y cuánto dinero le quedó?
-
Juan compró al comienzo del año, una caja con 48 colores,
al día de hoy ha perdido 4/8, de los colores. ¿Cuántos colores tiene aún Juan?
-
En una casa hay 12 integrantes, 4 de ellos se fueron de paseo.
¿Qué fracción de la familia se quedó
en casa ¿Qué fracción de la familia
salió de paseo?
ELEMENTOS
ESTADÍSTICOS
Población: es
el conjunto de todos los elementos a los que se les realiza un estudio
(colombianos, estudiantes del grado 4°, habitantes de Medellín…)
Muestra: corresponde
a la cantidad de individuos de la población a los cuales se les realizó el
estudio efectivo (cantidad de individuos a quienes se les realizó la encuesta).
Dato: cada
uno de los valores que se obtienen al realizar el estudio.
Variable: cada uno de las
características o cualidades que se estudian (la o las preguntas de la
encuesta)
Ejemplo:
A los estudiantes del grado 4° de la IEMFB, se le indagó frente a su
película favorita. las respuestas obtenidas, se registran en la siguiente tabla
de frecuencia.
Población: Estudiantes de 4° de la IEMFB (población general)
Muestra: 44 estudiantes (total de personas encuestadas)
Variable: Película favorita (pregunta)
Moda: Thor (dato con mayor frecuencia)
ACTIVIDAD
PARA PONER EN PRACTICA
Para cada una de las
siguientes tablas de frecuencia, elabora la gráfica de barras o de líneas y
puntos e identifica cada uno de los elementos estadísticos.
Para tener en cuenta: al elaborar la gráfica, en el eje X (horizontal), se escribe la variable descriptiva y en el eje Y(vertical), se escribe la variable numérica, de menor a mayor, partiendo del vértice o punto cero.
1-
A los habitantes del barrio pedregal, se le indagó frente
a su deporte preferido, los resultados se plasman en la siguiente tabla de
frecuencia.
Realizar gráfica de barras correspondiente a la información.
Completar:
Población
----------------
Muestra
------------------
Variable
------------------
Moda -------------------
-
2 - La selección del color
preferido en el grado preescolar, se representa en la siguiente tabla de
frecuencia
Realizar gráfica de líneas y puntos correspondiente a la información.
Completar:
Población
----------------
Muestra ------------------
Variable
------------------
Moda -------------------
¡Practiquemos
las operaciones básicas!
Resuelve de manera
vertical las siguientes operaciones:
-
1.203.546 - 235.102 =
-
-
48 + 125.241 + 352 =
-
-
45.235 ÷ 36 =
¡felicitaciones por tu esfuerzo!
RETO
CINCO
DURACIÓN:
octubre 26 – octubre 30
Fecha límite de entrega: martes 3 de noviembre
DBA: realiza sumas y restas de fracciones (utilizando
estrategias que muestran comprensión y no solo memorización de un
procedimiento).
En este reto
abordaremos: clases de fracciones, suma y resta de fracciones, clases de
cuadriláteros .
Recomendación: Antes de resolver la actividad , ver con atención los videos , leer comprensivamente los contenidos y analizar los ejemplos.
Clases de fracciones según su denominador
Las fracciones de acuerdo con su denominador, se
clasifican en Homogéneas y Heterogéneas.
Fracciones Homogénea
Son aquellas que tienen igual denominador, ejemplo
Adición
y sustracción de fracciones de igual denominador
Para sumar y /o restar
fracciones de igual denominador, se suman o se restan los numeradores y se escribe el mismo denominador,
ejemplo:
Suma:
Resta:
Fracciones heterogéneas
Son aquellas fracciones que tienen diferente denominador, ejemplo:
Adición
y sustracción de fracciones de diferente denominador.
Para sumar y/o restar fracciones de diferente
denominador, se pueden realizar diferentes procesos, en este caso, vamos a
trabajar el método de productos cruzados,
así:
- Para obtener el
numerador, se multiplica en equis(X), estos productos se suman o restan,
según el caso.
- Para obtener el denominador,
se multiplican los denominadores entre sí.
Ejemplo:
Suma:
Resta:
Para tener en cuenta
En la Resta, es necesario comenzar a multiplicar en equis(x),
por el numerador de la primera fracción, ya que no es lo mismo 8 – 3 que 3 – 8.
¡ vamos a poner en practica!
1 – Resuelvo las siguientes adiciones y sustracciones , identificando si son homogéneas o heterogéneas (deben aparecer los procesos)
- - 1/6 + 2/3 =
-
2/5 + 3/5 +1/5=
-
20/6 – 15/6 =
-
4/5 – 2/8 =
-
6/4 + 2/9 =
-
4/7 – 3/9 =
-
18/4 + 5/4 =
-
4/7 + 2/8 =
-
2 – resuelvo las siguientes situaciones (deben aparecer procesos y respuesta)
a – Para hacer una torta se
necesitan 3/5 de mantequilla y 8/5 de harina.¿ Qué fracción de los 2
ingredientes ,se necesita para la torta?
b- Andrés tiene 4/7 de cartulina y
juan tiene 6/6 de cartulina , si donan la cartulina que tienen , para
actividades del salón de clases. ¿Cuánta cartulina se recibe en el salón?.
c- Una modista dispone de 9/10 de
tela y utiliza 5/10 de la tela.¿ qué fracción de la tela queda sin utilizar?.
d- Marcela dispone de 8/3 de torta y
reparte entre sus amigos 4/2 de la torta.¿ qué fracción de la torta le queda a
Marcela?
Clases de cuadriláteros
Los cuadriláteros se clasifican en paralelogramos
y no paralelogramos, así:
Paralelogramos: son cuadriláteros cuyos lados son paralelos e iguales, dos a
dos.
No paralelogramos :. son cuadriláteros que solo tienen un par de lados paralelos o ninguno
Para recordar: líneas paralelas son aquellas
que siempre conservan la misma distancia (nunca se cortan)
¡para poner en practica!
En cada cuadrilátero , repasa del mismo color los
lados paralelos, después completa el cuadro.
|
CUADRILÁTERO |
LADOS PARALELOS (CANTIDAD) |
CLASE DE CUADRILÁTERO (PARALELOGRAMO O NO
PARALELOGRAMO |
|
A |
1 par de paralelas |
No paralelogramo |
|
B |
|
|
|
C |
|
|
|
D |
|
|
|
E |
|
|
|
F |
|
|
|
G |
|
|
¡felicitaciones , lo lograste
RETO SEIS
DURACIÓN: NOVIEMBRE NOVIEMBRE 9 - NOVIEMBRE 13
FECHA MÁXIMA DE ENTREGA : NOVIEMBRE 13
En este reto abordaremos la guía evaluativa de todo lo trabajado durante el tercer periodo.
Instrucciones :
1 - repasar todo lo trabajado en el periodo.
2 - las operaciones necesarias las realizas en el cuaderno (no hay que enviar).
3 - Seleccionar la respuesta correcta cuando estés seguro.
4 - Para resolver esta evaluación no habrá acompañamiento directo del docente , ya que es evaluativa (te ayudas de las notas y de los ejercicios resueltos con anterioridad).
5 -Dedicarle el tiempo y el esfuerzo necesario ,ya que esta evaluación tiene un valor muy alto dentro del periodo.
A continuación se comparte el link para resolver la guía ,
también se compartirá por los grupos de whatsapp(el
lunes 9 hay asesoría a la hora de costumbre).👇
https://docs.google.com/forms/d/1X_SSnr0JT_P2BlsYx4Ap6fqT4oZ6x5J1Z_yXmCm3zgU/edit?usp=sharing





































